lab历险记

 一、（bitXor）仅用~  (取反  )和&  (与)  实现x   ^(异或)   y

^：异或

按位异或的3个特点:
(1) 0 ^ 0=0,0 ^ 1=1 0异或任何数＝任何数
(2) 1 ^ 0=1,1 ^ 1=0 1异或任何数－任何数取反
(3) 任何数异或自己＝把自己置0

异或适用结合律和交换律
例如：

A ^ B = B ^ A
A ^ B ^ B = A ^ 0 = A

异或的应用：
①异或可以快速比较两个数的值，例如：A ^ A = 0要比A - A = 0来的快
②汇编语言中经常用于将变量置0，例如：xor a，a；
③用异或使某个特定的位翻转，例如：翻转1001 1100的第4位，只需将他和0000 1000异或即可
④判断一个二进制数中1的数量是奇数还是偶数，例如：

1001001：1 ^ 0 ^ 0 ^ 1 ^ 0 ^ 0 ^ 1 = 1
所以结果为1，是奇数，0是偶数

⑤不使用其他空间，交换两个值

①a = a ^ b;
b = a ^ b;代入①式 a ^ b ^ b = a ^ 0 = a;
a = a ^ b;类推
运用结合律和交换律

~：取反
是一元运算符，是将每个0变为1，将每个1变为0
。。。。。。。。。。。。。。。。。。。。。。。。。。。。
二进制的存储方式：计算机不直接存储二进制原码，而是存储二进制的补码。而正数的补码是原码，负数的补码是原码取反再加1.
那为什么输出-1的时候还是-1呢，而不是-1的补码呢
那是因为：

-1原码为：1000 0001，原码取反码再加一：1111 1111（即补码
而负数输出时，计算机将补码逆向译成原码
记住这句话：原码取反码再加一得补码，补码减一取反得原码

比如：

1
2

int a=7；
int b=~a；

得到的结果是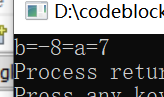

计算的方式：
a=0000 0111
①先取反得到：1111 1000（为b的补码
②计算机判断为负数，则减一再取反，先减一：1111 0111
③减一后再取反：1000 1000

有~n=-(n+1)

|：或运算
一个1为1，两个1也为1
做题思路：
笔者思路较浅，只能定义算法：x=4，y=5
先把x，y的取反，x与y，都写出来，然后一个一个进行计算得到x异或y的将结果即可

最终结果：

1
2
3

int bitXor(int x,int y){
	return ~(~x&~y)&~(x&y);
}

正确答案：

。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。
PS：进行位操作的时候是用补码操作的
因为在计算机系统中，数值一律用补码来表示和存储。
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。
异或运算：a ^ b = ~a & b | a & ~b

二、（tmin）返回补码整数的最小整数数值。

要求用到：! ~ & ^ | + << >>
做题前首先补充知识：
位操作符（进行位操作前需要转化位二进制

|：按位或；作用：一真则真；
例如：a=4；//0100 b=5；//0101 c=a | b = 0101
&：按位与；作用：一假则假；
例如：a=4；//0100 b=5；//0101 c=a & b = 0100
^： 按位异或；作用：相同为0，不同为1；
例如：a=4；//0100 b=5；//0101 c=a ^ b = 0001
~：按位取反见上
<<:数据左移；作用：5<<2向左移动2位
例如：a=5；//0101 a=a<<2；//010100
|>>:数据右移；作用：5>>2向有移动2位
例如：a=5；//0101 a=a>>2；//0001

逻辑操作符

&&：逻辑与；作用：两个操作数同时为真才为真，如果左边的操作数为假，则不会运行右边的操作数。
例如： int a=1,b=2,c=3,m=0,d=0,x=0;
d=(m=a==b)&&(x=c);
printf(“%d %d %d”,m,d,x);
结果：0，0，0
||：逻辑或；作用：两个操作数同时位假才为假，如果左边为真，则右边不运行；

单目运算符

！：不为0则变0，为0则变1
例如：a=2，b=0；a=!a;b=!b;//a=0,b=1
&：取变量的地址
例子：a=5,*p=&a;//p=5
*：取指针所指向变量的内容
例子：a=5,*p=&a;//p=5
在32位机器上，int型的最小值是0x7fffffff，也就是2,147,483,648，而最小值也就是-2,147,483,648

做题思路：

1
2

int i=(1<<31);
    return i; 

因为是32位，所以最小值就是符号位为1，数值位为0；

三、（isTmax）如果x是最大的二进制补码，返回1；否则，返回0

只能用：! ~ & ^ | +
最大的二进制补码是0x7fffffff，原码表示为-1

判断相等用异或，则有max==~（max+1），但要排除0xffffffff

1

return !(~(x^(x+1)))&!!(x +1);

不过我把int x改为了 unsigned int，因为无符号数的int，其0xffffffff也是最大值，有符号数的话，就是-1了。
&号左边用异或判断是否为max
右边排除0xffffffff

1
2
3
4
5
6
7
8
9
10
11
12
13

**int main() {
    int a = 0xffffffff;
    int b = 0x7fffffff;
    unsigned int j = 0xffffffff;
    printf("%u\t %d\n",a,a);
    printf("%d\n",b);
    printf("%u\n",j);
    printf("%d\n",-1);
    printf("%u",-1);
	return 0;
}
**

四、（allOddBits）判断一个二进制数奇数位是否全为1

取反后用补码运算
既然要判断奇数位全为1，那我们就要构造一个0xAAAAAAAA
就2 ^1、2 ^3是奇数位，不是在位置上数出来的

1
2
3
4
5

int y=0xA;
y=y+(y<<4);
y=y+(y<<8);
y=y+(y<<16);//y的奇数位全为1
return !((x&y)^y);

五、（negate）计算-x

1

return ~x+1;

~x+1能够实现变号，所以有 ~x+1 = -x很有用

六、（isAsciiDigit）判断x是否可以是表示数字的Ascii码；
若0x30 <= x <= 0x39，返回1

1

return !((x+(~0x30+1))>>31) & !((0x39+(~x+1))>>31);

由第五题得知~x+1 = -x，所以我们用这个来实现减法运算，在判断符号位就行（大减小，若为true，得1，&后return1）

七、（conditional）实现x?y:z

当x不为0时，!x=0，函数结果为y；当x不为0时，!x=0，函数结果为y

1
2
3
4
5
6
7

int main() { //这道题用到了三元运算符
    int x=0,y=2,z=3;
    int a=x?y:z;
    printf("%d",a);  //当x=0，输出3；x=1，输出2
	return 0;
}

本题代码：

1

return ((!x+~1+1)&y) | ((~!x+1)&z);

（补码运算不用转换，提醒自己）
|号左边，判断x是否等于1（让x-1）
右边判断是否为0

八、（isLessOrEqual）判断x<y；如果x<=y返回1否则返回0

先写出x和y的符号位，然后再符号位异或（判断是否相同（取反是为了能够最后return 1的值，因为异或相同为0），再来个y-x的符号位（也要取反，因为y-x>0的符号位是0），当符号位相同时，且y-x的符号位为0，return个&，就可以表示出1.第二个是判断x为正，y为负，直接可以返回0

1
2
3
4
5

int a=x>>31;//取x得符号位1
int b=y>>31;//取y得符号位
int c=!(a ^ b);//符号位相同为1，不同为0
int d=!((y+(~x+1))>>31);////取y-x得也就是大减小的符号位的相反，y>x得1，y<x得0
return  (d&c) | (!c&a);//左边符号相同:y>x返回1；右边符号不同:当x<0时返回1，x>0时返回0

九、（logicalNeg）实现！(按位非运算)就是使非0的数为0，为0的数为1.

~ （~x+1）和 ~ x，正好每个位都相反（非0时），&后全为0，然后和1&后，返回0.

为0时：&后为0x80000000，向右位移31位得到符号位，再和1&返回1

~x+1能够实现变号，所以有 ~x+1 = -x

~x 和 ~~x的原码位数值相反

1
2
3

int a=4;
int b=~a&~~a;
printf("%d",b);

那为何不用 ~ x和 ~~ x进行&运算呢，因为没法判断0（没法return 1）

1

return (((~x+1)|x)>>31)+1;

十、（howManyBits）判断二进制补码的最小位数

使用二分法：每次取一半，判断高位是否有1，有则至少需要16位，没有则取低16位的一半再次分析，以此类推。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

int y = x>>31;
  x =  (y & ~x) | (~y & x);//x为正则不变，为负则按位取反
  int a = !!(x>>16);//
  int a1 = a<<4;//若高16位有1，则计数16
  x >>=a1;//x向右移位16，继续重复操作
  int b = !!(x>>8);
  int b1 = b<<3;
  x >>=b1;
  int c = !!(x>>4);
  int c1 = c<<2;
  x >>=c1;
  int d = !!(x>>2);
  int d1 = d<<1;
  x >>=d1;
  int e = !!(x>>1);
  int e1 = e;
  x >>=e1;
  int f = !!x;
  int bits = a1 + b1 + c1 + d1 + e1 + f + 1;//+1是符号位
  return bits;

如果是一个正数，则需要找到它最高的一位（假设是 n）是 1 的，再加上符号位，结果为 n+1；如果是一个负数，则需要知道其最高的一位是 0 的（例如 4 位的 1101 和三位的 101 补码表示的是一个值：-3，最少需要 3 位来表示，也需要+1）

十一、（floatScale2）功能：对于入参 unsigned uf，以 float 来解释其二进制位，若 uf 为 NaN 或 无穷大 则直接返回，否则计算 uf * 2 并返回。

将数字乘二的操作：

1
2

s = x&（ 1 << 31）
x << 1 | s

首先排除无穷小、0、无穷大和非数值 NaN

1
2
3
4
5
6
7
8

int s,e,m;
s = uf&(1<<31);//符号位
e = (uf&0x7f800000)>>23;//阶码or指数
if (e==0) return uf <<1 | s;//指数为0，直接返回乘二的值
if (e==255) return uf;//无穷大直接返回
e++;//指数+1，相当于乘二
if (e==255) return 0x7f800000|s;//指数+1后为255，返回
return (e<<23) | (uf&0x807fffff);//否则返回指数+1后的原符号数

十二、（floatFloat2Int）传入一个无符号整数 uf，把它当作单精度浮点数，返回它截断后的整数部分。也就是 (int)uf。如果出现溢出，则返回 0x80000000u

为什么要将小数根据阶码与23的大小进行左右移位：
若阶码大于23，则等式右边2 ^x的x是要大于23的，而小数位转换为int型后，最大也就2的23次方，所以，当阶数大于23时，需要小数位向左移位（阶码-23）位

1
2
3
4
5
6
7
8
9
10
11
12

int s,e,x;
s = uf >> 31;//符号位
e = ((uf & 0x7f800000)>>23)-127;//真正的指数
x = (uf&0x007fffff)|0x00800000;//尾数且把省的1也加上了
if(!(uf&0x7fffffff)) return 0;//如果uf为0，则返回0
if(e > 31) return 0x80000000;//如果真正的指数>31，则返回溢出值
if(e < 0) return 0;//真正的指数小于零则返回零，因为0<原数<1
if(e > 23) x <<= (e - 23);//剩下考虑真正的指数和23的大小，进行移位
else x >>= (23 - e);
if(!((x >> 31)^s)) return x;如果符号相同直接返回原值，
else if (x>>31) return 0x80000000;//如果为负（原来为正），返回溢出值
else return ~x + 1;如果为正（原来为负），返回相反数

十三、（floatPower2）计算浮点数2.0^x；若结果太小返回0，太大返回 +INF

2.0的x方=（1.0x2的一次方）的x次方=1.0 x 2的x次方
所以 x 就当做真正的指数。
然后再考虑两个极端：①阶码<-127（导致0<num<1）②阶码>128（导致溢出）

1
2
3
4

int exp = x + 127;//把x当作真指数
if(exp <= 0) return 0;//此时0<原数<1，结果返回0
if(exp >= 255) return 0x7f800000;//此时溢出
return exp << 23;//否则x作为正常的指数